Schrödingergleichung
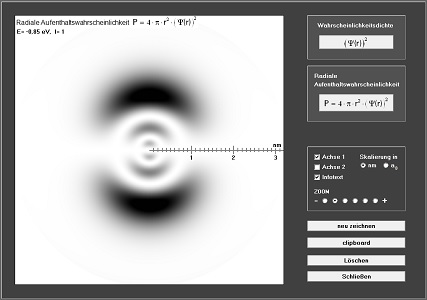
Dieses Programm löst die stationäre Schrödingergleichung des radialen Anteils der Wasserstoffwellenfunktion auf numerischen Weg und stellt die Wahrscheinlichkeitsdichten, Aufenthaltswahrscheinlichkeiten und Orbitale des Elektrons grafisch dar. Der Wert für die Gesamtenergie des Elektrons kann vom Anwender mit Hilfe von Schiebereglern beliebig gewählt werden. Der Drehimpuls darf die Werte 0,1,2,3 und 4 annehmen. Dass Programm liefert dann durch Lösen der Differentialgleichung eine entsprechende Wellenfunktion. Aber nur bei wenigen, ganz speziellen Energiewerten ergeben sich Funktionen, die gegen Null konvergieren und damit physikalisch sinnvolle Lösungen der Differentialgleichung darstellen. Diese Energiewerte werden Eigenwerte der Differentialgleichung genannt und entsprechen den vom Bohrschen Atommodell bekannten Energien des Wasserstoff-Termschemas.