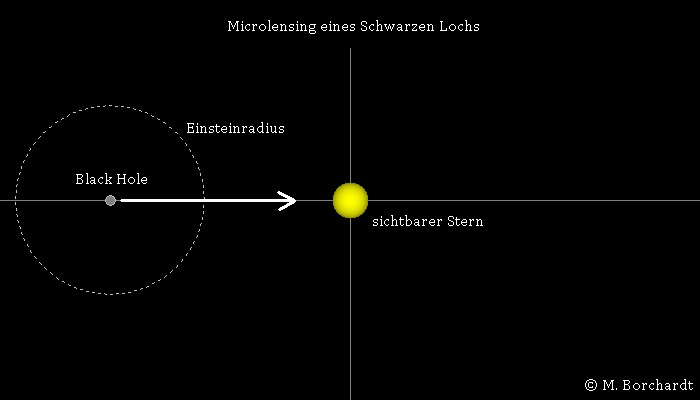
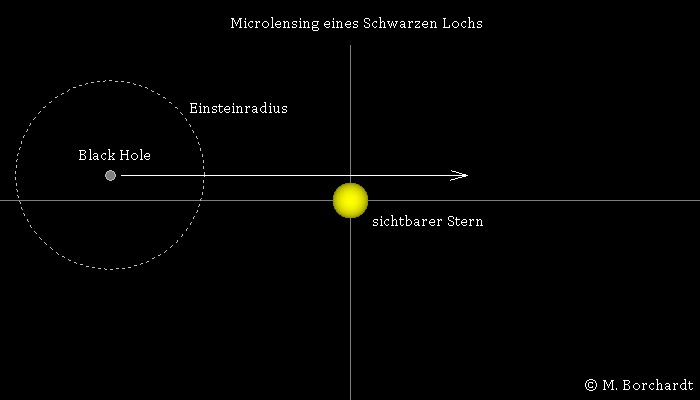
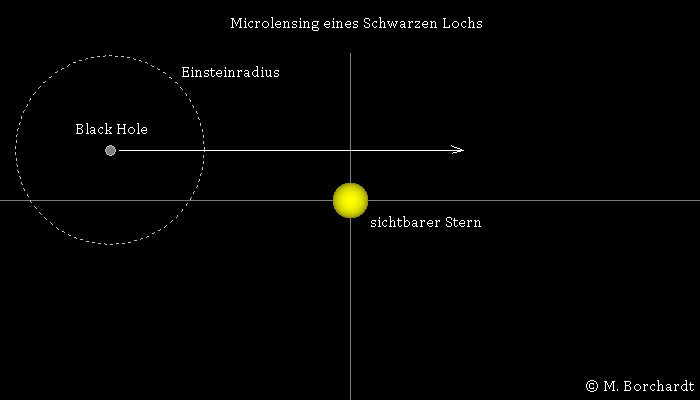
Microlensing-Ereignisse durch Stellare Schwarze Löcher
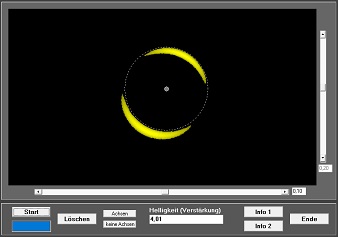
Kompakte Objekte, wie z.B. Schwarze Löcher, können als Gravitationslinsen wirken, d.h. sie können das Licht weit entfernter, hinter ihnen liegender Sterne derart ablenken, dass eine Lichtverstärkung auftritt.
Aufgrund der Rotation der galaktischen Scheibe kann es passieren, dass ein isoliertes, stellares Schwarzes Loch langsam vor einem weit entfernten Stern vorbeizieht. Das Programm berechnet, wie dann das Licht dieses Sterns durch die Gravitationswirkung des Schwarzen Lochs ablenkt wirkt. So entstehen Doppelbilder des Sterns und bei einer zentralen Passage sogar ein ausgeprägter Lichtring (Einstein-Ring). Die Skalierung der Koordinatenachsen wurde in Einheiten des Einsteinradius vorgenommen. Die Helligkeit der Abbildungen wird durch einfaches Aufaddieren der Pixel-Grauwerte bestimmt und ins Verhältnis zur Helligkeit des nicht deformierten Sternenlichts gesetzt, woraus sich dann die Lichtverstärkung ergibt.
Videos (Animationen) zu Microlensing-Ereignissen
Die Videos wurden mit Hilfe des oberen Programms "microlensing.exe" erzeugt. Ein Schwarzes Loch wandert vor einem Stern vorbei. Die Helligkeit des Sterns wurde für jedes Bild des Videos mithilfe des Programms ermittelt und als Lichtkurve dargestellt. So wird die Lichtverstärkung aufgrund des Gravitationslinseneffekts deutlich sichtbar.
Video 1: Ein Schwarzes Loch wandert zentral vor einem Stern vorbei (Stoßparameter p=0).
Video 2: Ein Schwarzes Loch wandert leicht versetzt vor einem Stern vorbei (Stoßparameter p=0,26).
Video 3: Ein Schwarzes Loch wandert deutlich versetzt vor einem Stern vorbei (Stoßparameter p=0,52).
Herleitung der Linsenformel und Parallaxen-Methode zur Bestimmung der Masse des SL
Das Dokument zeigt eine detaillierte Herleitung der Linsenformel für Microlensing-Ereignisse. Außerdem wird gezeigt, wie sich die Helligkeitskurve (Lichtverstärkung durch die Gravitationslinse) berechnen lässt und wie man die Masse des Schwarzen Lochs in einigen Fällen durch Parallaxeneffekte aufgrund der Bewegung der Erde um die Sonne berechnen kann. Das Dokument ist inhaltlich anspruchsvoll.
Download des PdF-Dokuments